超参数调试、Batch正则化和程序框架
超参数的调试处理
在机器学习领域,超参数比较少,我们之前利用设置网格点的方式来调试超参数;
但在深度学习领域,超参数较多,不再是设置规则的网格点,而是随机选择点进行调试。这样做是因为,在我们处理问题的时候,无法知道哪个超参数更为重要,随机的方式测试超参数点的性能更为合理,可以探究超参数的潜在价值。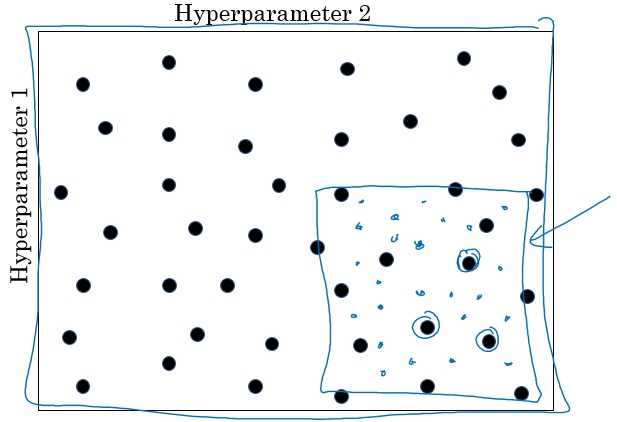
为超参数选择合适的范围
Scale 随机均匀取样
在超参数选择的时候,一些超参数是在一个范围内进行均匀随机取值,如隐藏层神经元结点的个数、隐藏层的层数等。但是有一些超参数的选择做均匀随机取值是不合适的,这里需要按照一定的比例在不同的小范围内进行均匀随机取值,以学习率 $\alpha$ 的选择为例,在 $0.001,\ldots,1$ 范围内进行选择:
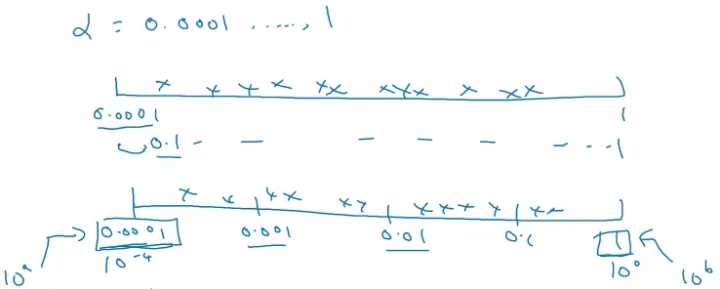
如上图所示,如果在 $0.001,\ldots,1$ 的范围内进行进行均匀随机取值,则有90% 的概率 选择范围在 $0.1\sim1$ 之间,而只有 10% 的概率才能选择到$0.001\sim0.1$ 之间,显然是不合理的。
所以在选择的时候,在不同比例范围内进行均匀随机取值,如 $0.001\sim0.001$ 、 $0.001\sim0.01$ 、 $0.01\sim0.1$ 、 $0.1\sim1$ 范围内选择。
代码实现
|
|
在 $10^{a}\sim10^{b}$ 之间的范围内进行随机均匀的选择,则 $r \in [a, b]$ , $\alpha = 10^{r}$ 。
类似地,在使用指数加权平均的时候,超参数 $\beta$ 也需要用这种方式进行随机均匀取样,选择合适的标尺来给超参数取值。
超参数调试实践: Pandas vs. Caviar
在超参数调试的实际操作中,我们需要根据我们现有的计算资源来决定以什么样的方式去调试超参数,进而对模型进行改进。下面是不同情况下的两种方式:
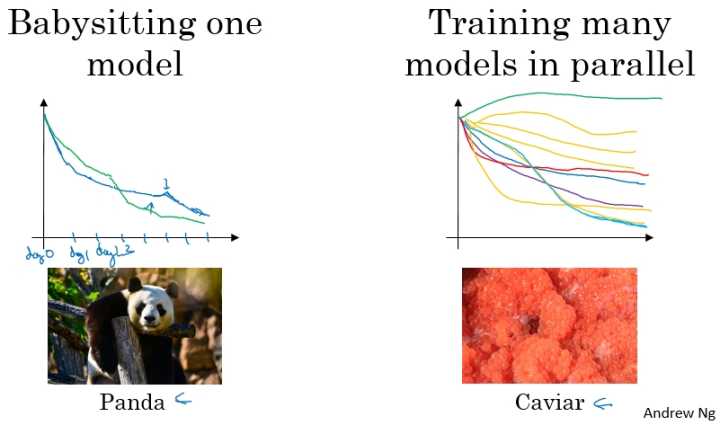
- 在计算资源有限的情况下,使用第一种(Pandas 方式),仅调试一个模型,每天不断优化;
- 在计算资源充足的情况下,使用第二种(Caviar 方式),同时并行调试多个模型,选取其中最好的模型。
归一化网络中激活值
在 Logistic Regression 中,将输入特征进行归一化,可以加速模型的训练。那么对于更深层次的神经网络,我们是否可以归一化隐藏层的输出 $a^{[l]}$ 或者经过激活函数前的 z^{[l]} ,以便加速神经网络的训练过程?答案是肯定的。
常用的方式是:将隐藏层经过激活函数激活前的 $z^{[l]}$ 进行归一化。
Batch Norm 的实现
以神经网络中某一隐藏层的中间值为例: $z^{(1)},z^{(2)},\ldots,z^{(m)}$ :
$$\mu = \dfrac{1}{m}\sum\limits_{i}z^{(i)}$$
$$\sigma^{2}=\dfrac{1}{m}\sum\limits_{i}(z^{(i)}-\mu)^{2}$$
$$z^{(i)}_{\rm norm} = \dfrac{z^{(i)}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}$$
这里加上 $\varepsilon$ 是为了保证数值的稳定。
到这里所有 $z$ 的分量都是平均值为 0 和方差为 1 的分布,但是我们不希望隐藏层的单元总是如此,也许不同的分布会更有意义,所以我们再进行计算:
$$\widetilde z^{(i)} = \gamma z^{(i)}_{\rm norm}+\beta$$
这里 $\gamma$ 和 $\beta$ 是可以更新学习的参数,如神经网络的权重 $w$ 一样,两个参数的值来确定 $\widetilde z^{(i)}$ 所属的分布。
$\widetilde z^{(i)}$ 来取代 $z^{(i)}$,方便NN中的后续计算。
归一化输入特征X是怎样有助于NN学习
Batch 归一化的归一化过程不仅适用于输入层,同样适用于NN中的深度隐藏层,不同的是,如果不想使隐藏层的均值为0、方差为1,这个就是为什么有了 $\gamma$ 和 $\beta$ 两个参数后,可以确保所有的$z^(i)$ 可以是你想赋予的任意值,或者说它的作用是保证隐藏单元已使均值和方差**标准化,均值和方差由这两个参数控制,使 $z^{(i)}$ 有固定的均值和方差**。
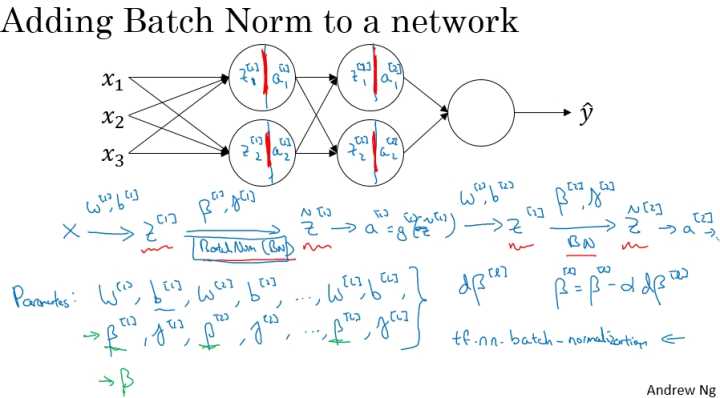
将 Batch Norm 融入神经网络中
在深度神经网络中应用 Batch Norm,这里以一个简单的神经网络为例,前向传播的计算流程如下图所示:
实现梯度下降
for t = 1 … num (这里num 为Mini Batch 的数量):
- 在每一个$X^{t}$上进行前向传播(forward prop)的计算:
- 在每个隐藏层都用 Batch Norm 将 $z^{[l]}$ 替换为 $\widetilde z^{[l]}$
- 使用反向传播(Back prop)计算各个参数的梯度: $dw^{[l]}$、$d\gamma^{[l]}$、$d\beta^{[l]}$
更新参数:
- $w^{[l]}:=w^{[l]}-\alpha dw^{[l]}$
- $\gamma^{[l]}:=\gamma^{[l]}-\alpha d\gamma^{[l]}$
- $\beta^{[l]}:=\beta^{[l]}-\alpha d\beta^{[l]}$
- 在每一个$X^{t}$上进行前向传播(forward prop)的计算:
与 Mini-batch 梯度下降法一样,Batch Norm 也适用于 Momentum、RMSprop、Adam 的梯度下降法来进行参数更新。
Notation
这里没有写出偏置参数 $b^{[l]}$ 是因为,对于式子 $z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}$ ,Batch Norm 要做的是将 $z^{[l]}$ 归一化,使其成为均值为0,标准差为1的分布,再由 $\beta$ 和 $\gamma$ 进行重新的分布缩放,那就是意味着:无论 $b^{[l]}$ 值为多少,在这个过程中都会被减去,不会再起作用。所以如果在神经网络中应用 Batch Norm 的话,可以直接将偏置参数 $b^{[l]}$ 去掉,或者将其置为零。
Batch Norm 起作用的原因
First Reason
首先 Batch Norm 可以加速神经网络训练。对输入层的输入特征进行归一化,从而改变Cost function的形状,使得每一次梯度下降都可以更快的接近函数的最小值点,从而加速模型训练过程的原理是有相同的道理。
Batch Norm 不仅仅将输入的特征进行归一化,而且将各个隐藏层的激活函数的激活值也进行归一化,并调整到另外的分布。
Second Reason
Batch Norm 有效的另外一个原因是它可以使权重比你的网络更滞后或者更深层。
下面是一个判别是否是猫的分类问题,假设第一训练样本的集合中的猫均是黑猫,而第二个训练样本集合中的猫是各种颜色的猫。如果我们将第二个训练样本直接输入到用第一个训练样本集合训练出的模型进行分类判别,那么我们在很大程度上是无法保证能够得到很好的判别结果。
这是因为第一个训练集合中均是黑猫,而第二个训练集合中各色猫均有,虽然都是猫,但是很大程度上样本的分布情况是不同的,所以我们无法保证模型可以仅仅通过黑色猫的样本就可以完美的找到完整的决策边界。第二个样本集合相当于第一个样本的分布的改变,称为:Covariate shift。如下图所示:
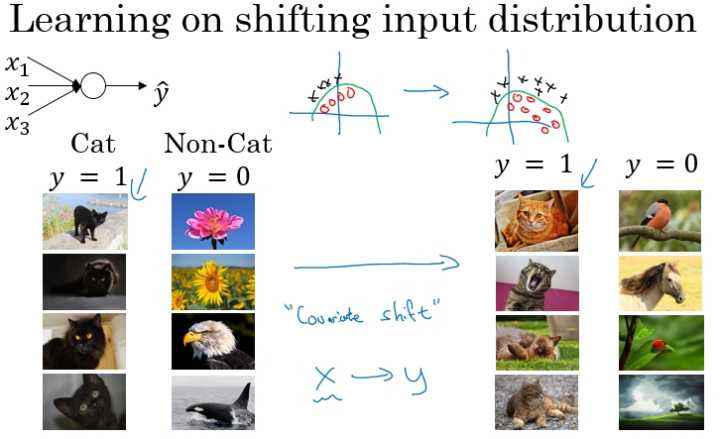
那么存在 Covariate shift 的问题如何应用在神经网络中?就是利用 Batch Norm 来实现。如下面的网络结构:
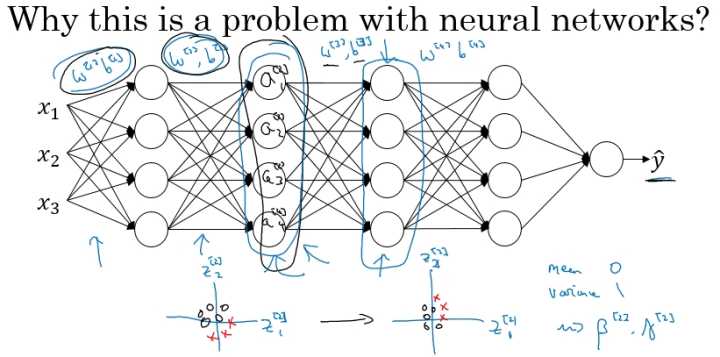
网络的目的是通过不断的训练,最后输出一个更加接近于真实值的 $\hat y$ 。现在以第2个隐藏层为输入来看:
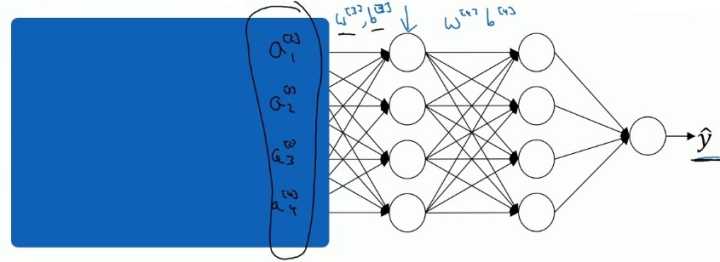
对于后面的神经网络,是以第二层隐层的输出值 $a^{[2]}$ 作为输入特征的,通过前向传播得到最终的 $\hat y$ ,但是因为我们的网络还有前面两层,由于训练过程,参数 $w^{[1]}$,$w^{[2]}$ 是不断变化的,那么也就是说对于后面的网络, $a^{[2]}$ 的值也是处于不断变化之中,所以就有了Covariate shift的问题。
那么如果对 $z^{[2]}$ 使用了 Batch Norm,那么即使其值不断的变化,但是其均值和方差却会保持。那么 Batch Norm 的作用便是其减少了输入值改变的问题,限制了前层的参数更新导致会影响数值分布的程度,使得网络的后层变得更加稳定。另一个角度就是可以看作,Batch Norm 减弱了前层参数与后层参数之间的联系,使得网络的每层都可以自己进行学习,相对其他层有一定的独立性,这会有助于加速整个网络的学习。
Batch Norm 正则化效果
Batch Norm 还有轻微的正则化效果。
- 这是因为在使用Mini-batch梯度下降的时候,每次计算均值和方差都是在一个Mini-batch上进行计算,而不是在整个数据样集上。这样就在均值和方差上带来一些比较小的噪声。
- 因为mini-batch是由一小部分数据估计得来的,在 $z^{[2]}$ 到 $\widetilde z^{[l]}$ 过程也会有一些噪声,因为它是用有些噪声的均值和方差计算得来的。所以和 Dropout 相似,其在每个隐藏层的激活值上加入了一些噪声,(这里因为Dropout 以一定的概率给神经元乘上0或者1)。所以类似于Dropout,Batch Norm 也有轻微的正则化效果,使得下游单元不过分依赖任何一个上游单元。
- 因为只是引入轻微的正则化效果,所以Batch Norm可以和Dropout一起使用
这里有一个小的细节就是,如果使用Batch Norm ,那么使用大的Mini-batch如512,相比使用小的Mini-batch(如64),会引入更少的噪声,那么就会减少正则化的效果。
测试阶段的 Batch Norm
训练过程中,我们是在每个 Mini-batch 使用 Batch Norm,来计算所需要的均值 $\mu$ 和方差 $\sigma^{2}$ 。但是在测试的时候,我们需要对每一个测试样本进行预测,无法计算均值和方差。
此时,我们需要单独进行估算均值 $\mu$ 和方差 $\sigma^{2}$ 。通常的方法就是在我们训练的过程中,对于训练集的 Mini-batch,使用指数加权平均(也叫流动平均 ),当训练结束的时候,得到指数加权平均后的均值 $\mu$ 和方差 $\sigma^{2}$ ,而这些值直接用于 Batch Norm 公式的计算,用以对测试样本进行预测。

Softmax 回归
在多分类问题中,有一种 logistic regression 的一般形式,叫做 Softmax regression。Softmax 回归可以将多分类任务的输出转换为各个类别可能的概率,从而将最大的概率值所对应的类别作为输入样本的输出类别。
计算公式
下图是 Softmax 的公式以及一个简单的例子:
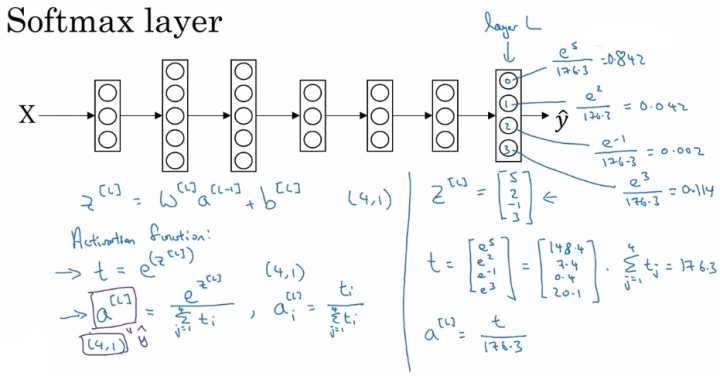
可以看出Softmax通过向量 $z^{[L]}$ 计算出总和为1的四个概率。
在没有隐藏层的时候,直接对 Softmax 层输入样本的特点,则在不同数量的类别下,Sotfmax 层的作用:
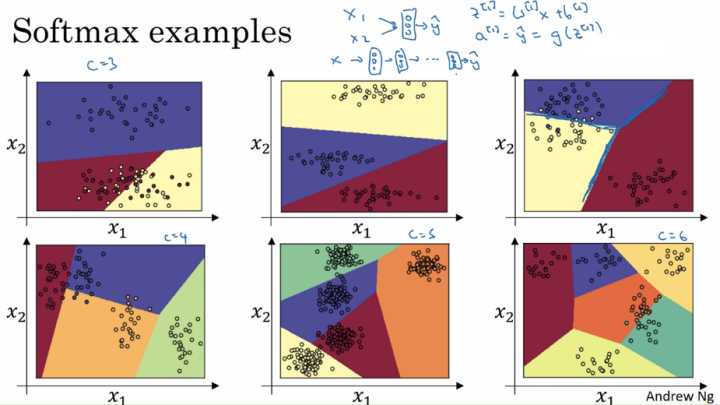
训练 Sotfmax 分类器
理解 Sotfmax
为什么叫做Softmax?我们以前面的例子为例,由 $z^{[L]}$ 到 $a^{[L]}$ 的计算过程如下:

通常我们判定模型的输出类别,是将输出的最大值对应的类别判定为该模型的类别,也就是说最大值为的位置1,其余位置为0,这也就是所谓的“hard max”。而Sotfmax将模型判定的类别由原来的最大数字5,变为了一个最大的概率0.842,这相对于“hard max”而言,输出更加“soft”而没有那么“hard”。
Sotfmax回归 将 logistic回归 从二分类问题推广到了多分类问题上。
Softmax 的 Loss function
在使用Sotfmax层时,对应的目标值 y 以及训练结束前某次的输出的概率值 $\hat y$ 分别为:
$$y=\left[ \begin{array}{l} 0\1\0\0 \end{array} \right] , \ \hat y=\left[ \begin{array}{l} 0.3\0.2\0.1\0.4 \end{array} \right]$$
Sotfmax使用的 Loss function 为:
$$L(\hat y,y)=-\sum\limits{j=1}^{4}y{j}\log \hat y_{j}$$
在训练过程中,我们的目标是最小化Loss function,由目标值我们可以知道, $y{1}=y{3}=y{4}=0, y{2}=1$ ,所以代入 $L(\hat y,y)$ 中,有:
$$L(\hat y,y)=-\sum\limits{j=1}^{4}y{j}\log \hat y{j}=-y{2}\log \hat y{2}=-\log \hat y{2}$$
所以为了最小化Loss function,我们的目标就变成了使得 $\hat y_{2}$ 的概率尽可能的大。
也就是说,这里的损失函数的作用就是找到你训练集中真实的类别,然后使得该类别相应的概率尽可能地高,这其实是最大似然估计的一种形式。
对应的Cost function如下:
$$J(w^{[1]},b^{[1]},\ldots)=\dfrac{1}{m}\sum\limits_{i=1}^{m}L(\hat y^{(i)},y^{(i)})$$
Softmax 的梯度下降
在Softmax层的梯度计算公式为:
$$\dfrac{\partial J}{\partial z^{[L]}}=dz^{[L]} = \hat y -y$$
深度学习框架

Tensorflow

[1] 吴恩达网络云课堂 deeplearning.ai 课程
