优化算法
Mini-batch 梯度下降法
对整个训练集进行梯度下降法的时候,我们必须处理整个训练数据集,然后才能进行一步梯度下降,即每一步梯度下降法需要对整个训练集进行一次处理,如果训练数据集很大的时候,如有500万或5000万的训练数据,处理速度就会比较慢。
但是如果每次处理训练数据的一部分,即用其子集进行梯度下降,则我们的算法速度会执行的更快。而处理的这些一小部分训练子集即称为 Mini-batch。
算法核心

对于普通的梯度下降法,一个 epoch(一代,遍历一词训练集) 只能进行一次梯度下降;而对于 Mini-batch 梯度下降法,一个 epoch 可以进行 $\frac{m}{Mini-batch}$ 个梯度下降(m为训练集总数)。
不同size大小的比较
普通的batch梯度下降法和 Mini-batch 梯度下降法代价函数的变化趋势,如下图所示:
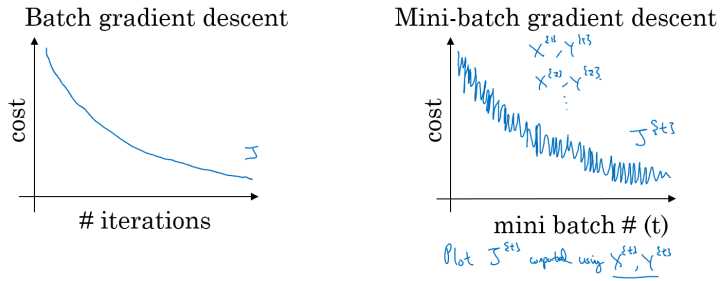
batch梯度下降:
- 对所有m个训练样本($size = m$)执行一次梯度下降,单次迭代耗时太长;
- Cost function 总是向减小的方向下降。
随机梯度下降:
- 对每一个训练样本($size = 1$)执行一次梯度下降,但是丢失了向量化带来的计算加速;
- Cost function总体的趋势向最小值的方向下降,但是无法到达全局最小值点,呈现波动的形式。
Mini-batch梯度下降:
- 选择一个 $1<size<m$ 的合适的size进行Mini-batch梯度下降,可以实现快速学习,也应用了向量化带来的好处;
- Cost function的下降处于前两者之间。

Mini-batch 大小的选择
- 如果训练样本的大小比较小时( $m\leqslant 2000$ 时): 选择batch梯度下降法;
- 如果训练样本的大小比较大时,典型的大小为: $2^{6}$、$2^{7}$、$\cdots$、$2^{10}$ (常用64,128, 256,512);
- Mini-batch的大小要符合CPU/GPU内存。
指数加权平均
指数加权平均的关键函数:
$$v{t} = \beta v{t-1}+(1-\beta)\theta_{t}$$
下图是一个关于天数和温度的散点图:
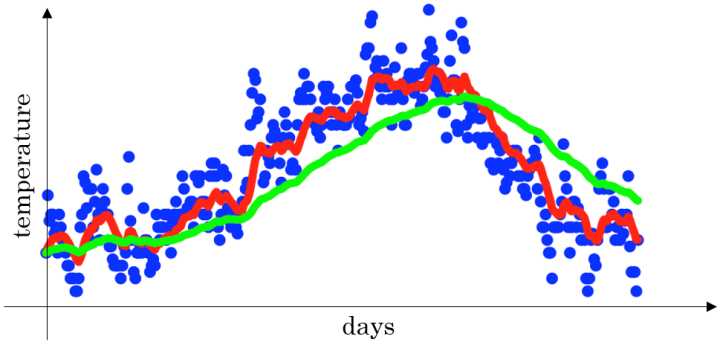
- 当 $\beta$ =0.9 时,指数加权平均最后的结果如图中红色线所示;
- 当 $\beta$ =0.98 时,指数加权平均最后的结果如图中绿色线所示;
- 当 $\beta$ =0.5 时,指数加权平均最后的结果如下图中黄色线所示;
理解指数加权平均
例子,当 $\beta$ =0.9 时:
$$v{100} = 0.9v{99}+0.1\theta{100}$$
$$v{99} = 0.9v{98}+0.1\theta{99}$$
$$v{98} = 0.9v{97}+0.1\theta_{98}$$
$$\ldots$$
展开,有:
$$v{100}=0.1\theta{100}+0.9(0.1\theta{99}+0.9(0.1\theta{98}+0.9v{97}))$$
$$=0.1\theta{100}+0.1\times0.9\theta{99}+0.1\times(0.9)^{2}\theta{98}+0.1\times(0.9)^{3}\theta_{97}+\cdots$$
上式中所有 $\theta$ 前面的系数相加起来为1或者接近于1, 这叫做指数加权移动平均。
总体来说存在, $(1-\varepsilon)^{1/\varepsilon}=\dfrac{1}{e}$ ,在我们的例子中, $1-\varepsilon=\beta=0.9$ ,即 $0.9^{10}\approx 0.35\approx\dfrac{1}{e}$ 。相当于大约10天后,系数的峰值(这里是0.1)下降到原来的 $\dfrac{1}{e}$ ,只关注了过去10天的天气。
指数加权平均实现
$$v{0} =0$$
$$ v{1}= \beta v{0}+(1-\beta)\theta{1}$$
$$ v{2}= \beta v{1}+(1-\beta)\theta{2}$$
$$ v{3}= \beta v{2}+(1-\beta)\theta{3}$$
$$ \ldots$$
因为,在计算当前时刻的平均值,只需要前一天的平均值和当前时刻的值,所以在数据量非常大的情况下,指数加权平均在节约计算成本的方面是一种非常有效的方式,可以很大程度上减少计算机资源存储和内存的占用。
指数加权平均的偏差修正
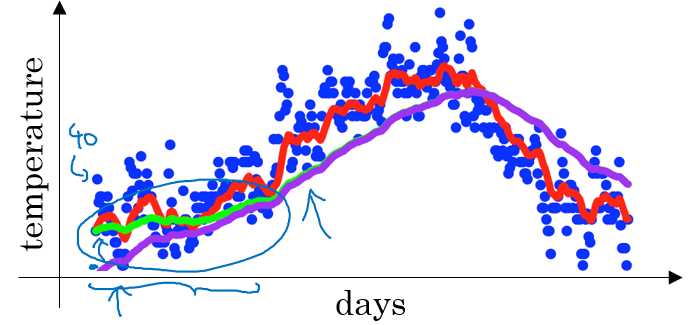
在我们执行指数加权平均的公式时,当 $\beta$=0.98 时,我们得到的并不是图中的绿色曲线,而是下图中的紫色曲线,其起点比较低。
- 原因:
$$v{0}=0$$
$$v{1}=0.98v{0}+0.02\theta{1}=0.02\theta{1}$$
$$v{2}=0.98v{1}+0.02\theta{2}
=0.98\times0.02\theta{1}+0.02\theta{2}
=0.0196\theta{1}+0.02\theta{2}$$
如果第一天的值为如 40 ,则 $v_{1}=0.02\times40=8$ ,得到的值要远小于实际值,后面几天的情况也会由于初值引起的影响,均低于实际均值。
- 偏差修正:
不直接使用 $v{t}$,而是使用 $\frac{v{t}}{1- \beta^{t}}$
使用 $v_{1}=0.02\times40=8$
当 t=2 时:
$$1-\beta^{t}=1-(0.98)^{2}=0.0396$$
$$\dfrac{v{2}}{0.0396}=\dfrac{0.0196\theta{1}+0.02\theta_{2}}{0.0396}$$
偏差修正得到了绿色的曲线,在开始的时候,能够得到比紫色曲线更好的计算平均的效果。随着 t 逐渐增大, $\beta^{t}$ 接近于0,所以后面绿色的曲线和紫色的曲线逐渐重合了。
虽然存在这种问题,但是在实际过程中,一般会忽略前期均值偏差的影响。
动量(Momentum)梯度下降法
动量梯度下降的基本思想就是计算梯度的指数加权平均数,并利用该梯度来更新权重。
在我们优化 Cost function 的时候,以下图所示的函数图为例:
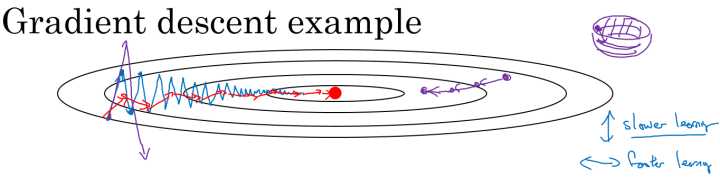
在利用梯度下降法来最小化该函数的时候,每一次迭代所更新的代价函数值如图中蓝色线所示在上下波动,而这种幅度比较大波动,减缓了梯度下降的速度,而且我们只能使用一个较小的学习率来进行迭代。
如果用较大的学习率,结果可能会如紫色线一样偏离函数的范围,所以为了避免这种情况,只能用较小的学习率。
但是我们又希望在如图的纵轴方向梯度下降的缓慢一些,不要有如此大的上下波动,在横轴方向梯度下降的快速一些,使得能够更快的到达最小值点,而这里用动量梯度下降法既可以实现,如红色线所示。
算法实现
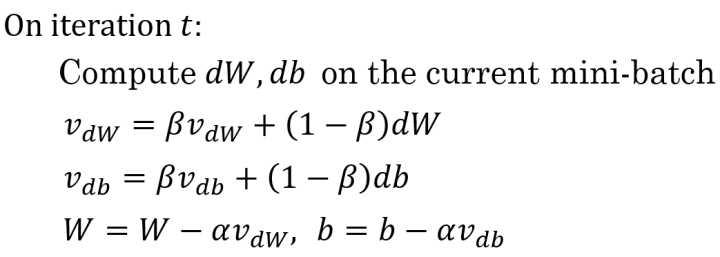
其中,$\alpha, \beta$ 为超参数,且 $\beta$ 常用的值是0.9。
在我们进行动量梯度下降算法的时候,由于使用了指数加权平均的方法。原来在纵轴方向上的上下波动,经过平均以后,接近于0,纵轴上的波动变得非常的小;但在横轴方向上,所有的微分都指向横轴方向,因此其平均值仍然很大。最终实现红色线所示的梯度下降曲线。
算法本质解释
在对应上面的计算公式中,将Cost function想象为一个碗状,想象从顶部往下滚球,其中:
- 微分项 dw,db 想象为球提供的加速度;
- 动量项 $v{dw}$,$v{db}$ 相当于速度;
小球在向下滚动的过程中,因为加速度的存在使得速度会变快,但是由于 $\beta$ 的存在,其值小于1,可以认为是摩擦力,所以球不会无限加速下去。
RMSprop
除了上面所说的 Momentum 梯度下降法,RMSprop(root mean square prop,均方根)也是一种可以加快梯度下降的算法(两者都可以消除梯度下降过程中的摆动)。
同样算法的样例实现如下图所示:
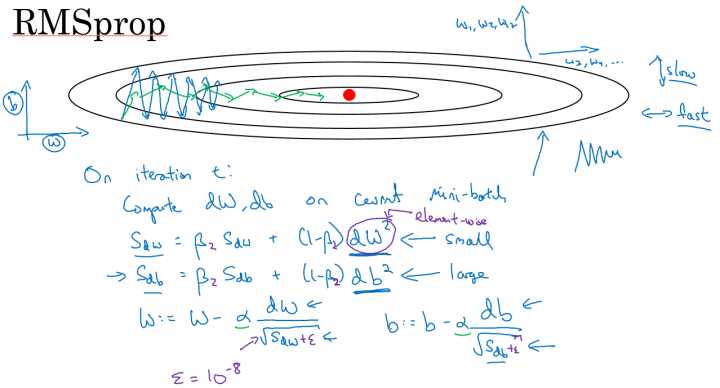
这里假设参数b的梯度处于纵轴方向,参数 w 的梯度处于横轴方向(当然实际中是处于高维度的情况),利用 RMSprop 算法,可以减小某些维度梯度更新波动较大的情况,如图中蓝色线所示,使其梯度下降的速度变得更快,如图绿色线所示。
在如图所示的实现中,RMSprop 将微分项进行平方,然后使用平方根进行梯度更新,同时为了确保算法不会除以 0,平方根分母中在实际使用会加入一个很小的值如 $\varepsilon=10^{-8}$ 。
Adam 优化算法
Adam (Adaptive Moment Estimation)优化算法的基本思想就是将 Momentum 和 RMSprop 结合起来形成的一种适用于不同深度学习结构的优化算法。
算法实现
- 初始化: V{dw} = 0,S{dw}=0,V{db}=0,S{db} = 0
- 第 t 次迭代:
- Compute dw,db on the current mini-batch
- $V{dw} = \beta{1}V{dw}+(1-\beta{1})dw, V{db} = \beta{1}V{db}+(1-\beta{1})db$ <— “Momentum”
- $S{dw}=\beta{2}S{dw}+(1-\beta{2})(dw)^{2}, S{db}=\beta{2}S{db}+(1-\beta{2})(db)^{2}$ <— “RMSprop”
- $V{dw}^{corrected} = V{dw}/(1-\beta{1}^{t}),V{db}^{corrected} = V{db}/(1-\beta{1}^{t})$ <— 偏差修正
- $S{dw}^{corrected} = S{dw}/(1-\beta{2}^{t}), S{db}^{corrected} = S{db}/(1-\beta{2}^{t})$ <— 偏差修正
- $w:=w-\alpha\dfrac{V{dw}^{corrected}}{\sqrt{S{dw}^{corrected}}+\varepsilon}, b:=b-\alpha\dfrac{V{db}^{corrected}}{\sqrt{S{db}^{corrected}}+\varepsilon}$
超参数的选择
- $\alpha$ :需要进行调试;
- $\beta_{1}$ :常用缺省值为0.9, dw 的加权平均;
- $\beta_{2}$ :推荐使用0.999, $dw^{2}$ 的加权平均值;
- $\varepsilon$ :推荐使用 $10^{-8}$ 。
学习率衰减
在我们利用 mini-batch 梯度下降法来寻找Cost function的最小值的时候,如果我们设置一个固定的学习速率 $\alpha$ ,则算法在到达最小值点附近后,由于不同batch中存在一定的噪声,使得不会精确收敛,而一直会在一个最小值点较大的范围内波动,如下图中蓝色线所示。
但是如果我们使用学习率衰减,逐渐减小学习速率 $\alpha$ ,在算法开始的时候,学习速率还是相对较快,能够相对快速的向最小值点的方向下降。但随着 $\alpha$ 的减小,下降的步伐也会逐渐变小,最终会在最小值附近的一块更小的区域里波动,如图中绿色线所示。
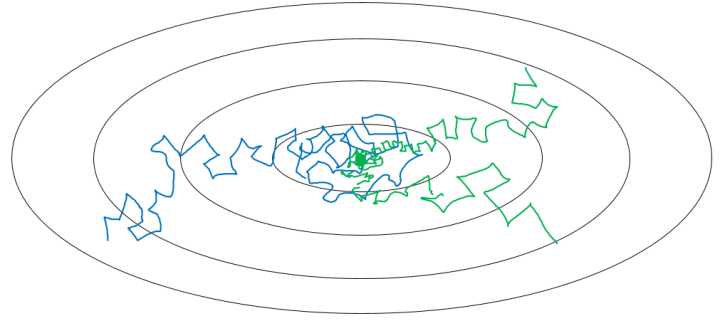
学习率衰减的实现
- 常用: $\alpha = \dfrac{1}{1+decay_rate*epoch_num}\alpha_{0}$
- 指数衰减: $\alpha = 0.95^{epoch_num}\alpha_{0}$
- 其他: $\alpha = \dfrac{k}{epoch_num}\cdot\alpha_{0}$
- 离散下降(不同阶段使用不同的学习速率)
局部最优问题
在低维度的情形下,我们可能会想象到一个Cost function 如左图所示,存在一些局部最小值点,在初始化参数的时候,如果初始值选取的不得当,会存在陷入局部最优点的可能性。
但是,如果我们建立一个高维度的神经网络。通常梯度为零的点,并不是如左图中的局部最优点,而是右图中的鞍点(叫鞍点是因为其形状像马鞍的形状)。
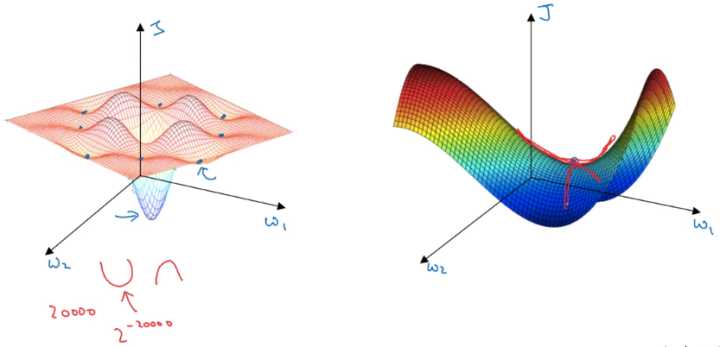
在一个具有高维度空间的函数中,如果梯度为0,那么在每个方向,Cost function可能是凸函数,也有可能是凹函数。但如果参数维度为2万维,想要得到局部最优解,那么所有维度均需要是凹函数,其概率为 $2^{-20000}$ ,可能性非常的小。也就是说,在低维度中的局部最优点的情况,并不适用于高维度,在梯度为0的点更有可能是鞍点,而不是局部最小值点。
在高纬度的情况下:
- 几乎不可能陷入局部最小值点;
- 处于鞍点的停滞区会减缓学习过程,利用如Adam等算法进行改善。
[1] 吴恩达网络云课堂 deeplearning.ai 课程
