深层神经网络
矩阵的维度
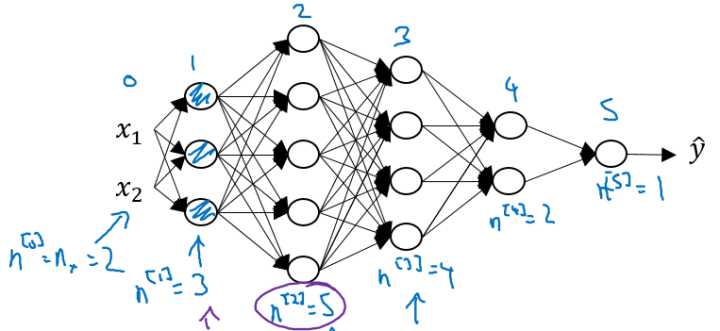
DNN结构示意图如图所示:
$$W^{[l]}: (n^{[l]},n^{[l-1]})$$
$$b^{[l]}: (n^{[l]},1)$$
在运算过程中,使用python的“广播”将$b^{[1]}$复制为$(n^{[l]}, m)$,m为训练集大小
$$dW^{[l]}: (n^{[l]},n^{[l-1]})$$
$$db^{[l]}: (n^{[l]},1)$$
$$Z^{[l]}: (n^{[l]},1)$$
$$
A^{[l]}=Z^{[l]}: (n^{[l]},1)
$$
为什么使用深层表示
人脸识别和语音识别:
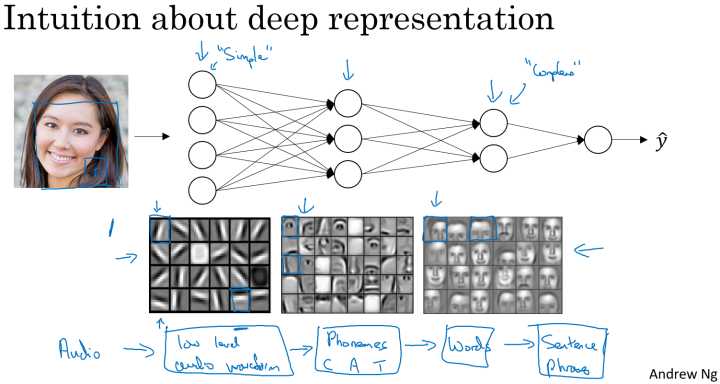
对于人脸识别,神经网络的第一层从原始图片中提取人脸的轮廓和边缘,每个神经元学习到不同边缘的信息;网络的第二层将第一层学得的边缘信息组合起来,形成人脸的一些局部的特征,例如眼睛、嘴巴等;后面的几层逐步将上一层的特征组合起来,形成人脸的模样。随着神经网络层数的增加,特征也从原来的边缘逐步扩展为人脸的整体,由整体到局部,由简单到复杂。层数越多,那么模型学习的效果也就越精确。
对于语音识别,第一层神经网络可以学习到语言发音的一些音调,后面更深层次的网络可以检测到基本的音素,再到单词信息,逐渐加深可以学到短语、句子。
所以从上面的两个例子可以看出随着神经网络的深度加深,模型能学习到更加复杂的问题,功能也更加强大。
电路逻辑计算:
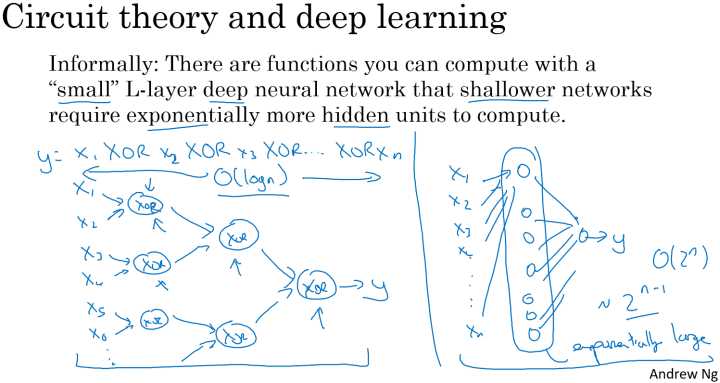
假定计算异或逻辑输出:
$$
y = x{1}\oplus x{2}\oplus x{3}\oplus \cdots\oplus x{n}
$$
对于该运算,若果使用深度神经网络,每层将前一层的相邻的两单元进行异或,最后到一个输出,此时整个网络的层数为一个树形的形状,网络的深度为 $O(\log_{2}(n))$ ,共使用的神经元的个数为:
$$
1+2+\cdot+2^{\log{2}(n)-1} = 1\cdot \dfrac{1-2^{\log{2}(n)}}{1-2} = 2^{\log_{2}(n)}-1 = n-1
$$
即输入个数为n,输出个数为n-1。
但是如果不使用深层网络,仅仅使用单隐层的网络(如图右侧所示),需要的隐层神经元个数为 $2^{n-1}$ 个 。同样的问题,但是深层网络要比浅层网络所需要的神经元个数要少得多。
前向和反向传播
首先给定DNN的一些参数:
L:DNN的总层数;
$n^{[l]}$:表示第 l 层的包含的单元个数;
$a^{[l]}$ :表示第 l 层激活函数的输出;
$W^{[l]}$ :表示第 l 层的权重;
输入 x 记为 $a^{[0]}$ ,输出 $\hat y$ 记为 $a^{[L]}$ 。
前向传播(Forward propagation)
Input: $a^{[l-1]}$
Output: $a^{[l]}$ , $\rm cache(z^{[l]})$
公式:
$$z^{[l]}= W^{[l]}\cdot a^{[l-1]}+b^{[l]}$$
$$a^{[l]}=g^{[l]}(z^{[l]})$$
向量化程序:
$$Z^{[l]}=W^{[l]}\cdot A^{[l-1]}+b^{[l]}$$
$$A^{[l]}=g^{[l]}(Z^{[l]})$$
反向传播(Backward propagation)
Input: $da^{[l]}$
Output: $da^{[l-1]}$ , $dW^{[l]}$ ,$db^{[l]}$
公式:
$$dz^{[l]}=da^{[l]} * g^{[l]}{‘}(z^{[l]})$$
$$dW^{[l]}=dz^{[l]}\cdot a^{[l-1]}$$
$$db^{[l]}=dz^{[l]}$$
$$da^{[l-1]}=W^{[l]}{^T}\cdot dz^{[l]}$$
将 $da^{[l-1]}$ 代入 $dz^{[l]}$ ,有:
$$dz^{[l]}=W^{[l+1]}{^T}\cdot dz^{[l+1]}* g^{[l]}{‘}(z^{[l]})$$
向量化程序:
$$dZ^{[l]}=dA^{[l]} * g^{[l]}{‘}(Z^{[l]})$$
$$dW^{[l]}=\dfrac{1}{m}dZ^{[l]}\cdot A^{[l-1]}$$
$$db^{[l]}=\dfrac{1}{m}np.sum(dZ^{[l]},axis=1,keepdims = True)$$
$$dA^{[l-1]}=W^{[l]}{^T}\cdot dZ^{[l]}$$
参数和超参数
参数:参数即是我们在过程中想要模型学习到的信息, $W^{[l]}$ , $b^{[l]}$ 。
超参数:超参数即为控制参数的输出值的一些网络信息,也就是超参数的改变会导致最终得到的参数 $W^{[l]}$ , $b^{[l]}$ 的改变。
举例:
学习速率:$\alpha$
迭代次数: N
隐藏层的层数:L
每一层的神经元个数: $n^{[1]}$ ,$ n^{[2]}$ , $\cdots$
激活函数 g(z) 的选择
更多超参数的调整和学习吴恩达老师将在下一个主题中介绍。
[1] 吴恩达网络云课堂 deeplearning.ai 课程